迟到的元旦快乐

序

在元旦之前，本想炫技生成漂亮的数独图案的题目然后发在朋友圈祝朋友们节日快乐。可惜是技术实在不过关。

数独图形

在资深的数独迷眼里,标准数独是指通过盘面上的所有提示数字，有且仅有唯一解。
以下四个图形，虽说有“元旦快乐”的四个字样，但是并不具备唯一解。

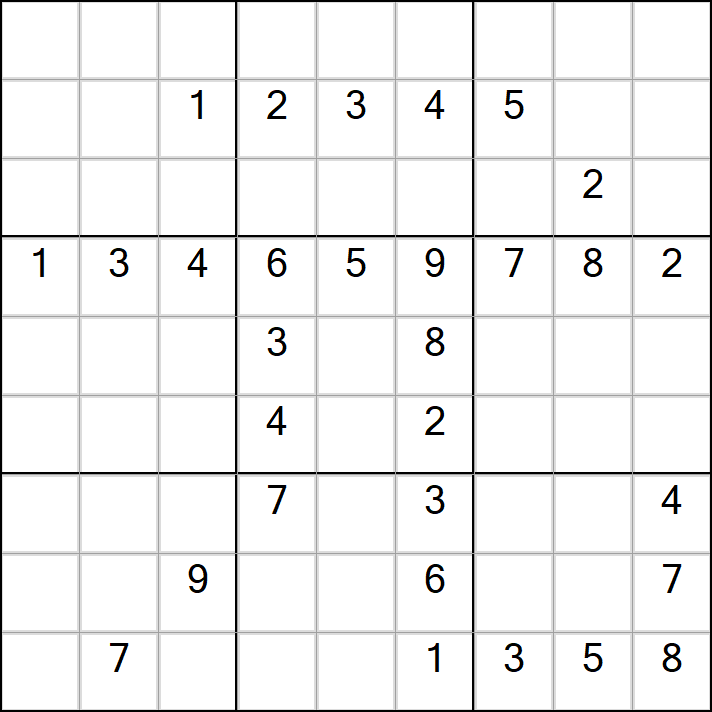
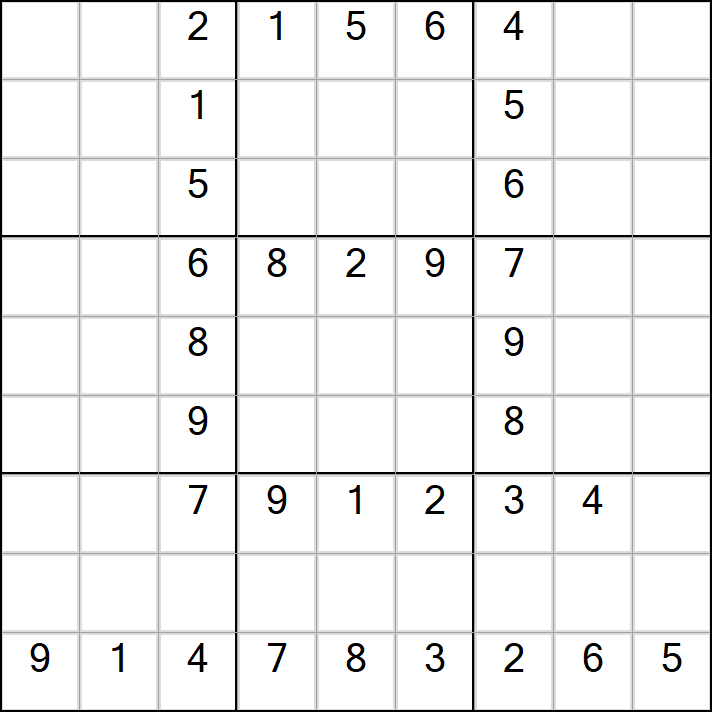
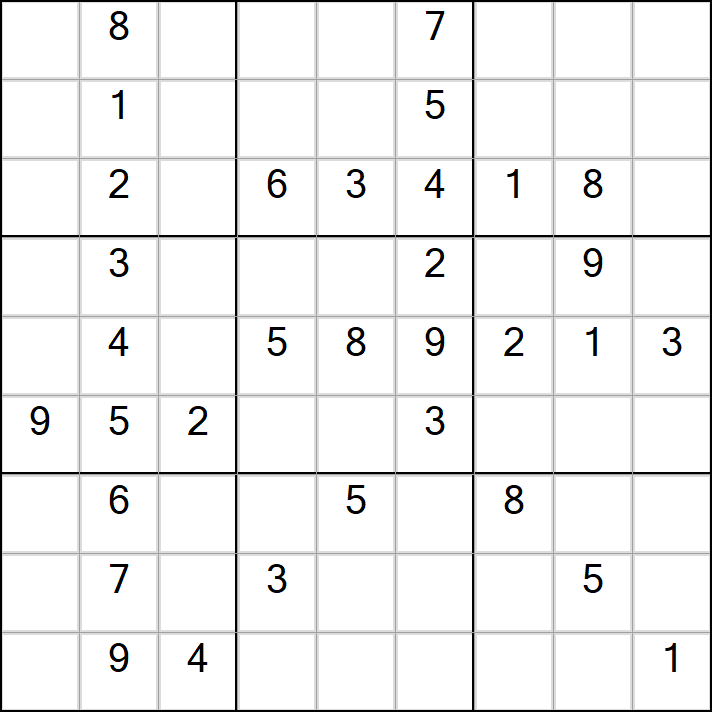
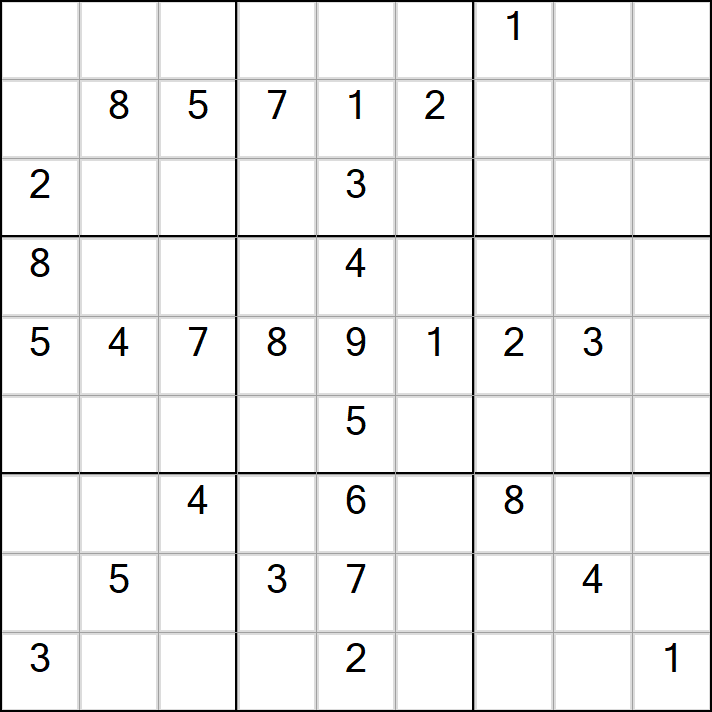
我们可以经由DLX算法可以快速得知
以上“元旦快乐”四个数字的可能解的个数是分别是512,8388,66,285。

标准数独的基本条件

盘面至少17个数字。
每一大行中没有两个空行,即第一，二，三行必须有两行存在数字。
每一大列中没有两个空列,即第一，二，三列必须有两列存在数字。
盘面至少有8个不同的已知数字。
即元字的r3c8会有个2的存在是为了避免第一和第三行可以互换,不满足数独唯一性的必要条件。

求解过程

以元字的表达式为例

// 元表达式
var before = new DanceLink().solution_count("000000000001234500000000020134659782000308000000402000000703004009006007070001358");
// 元的第一个已知数据和第二个已知数据交换
var after  = new DanceLink().solution_count("000000000002134500000000020134659782000308000000402000000703004009006007070001358");

输出的结果是

before = 512;
after  = 312;

所以最终解可以由after的表达式进行进一步的两两交换去生成。
由因为A的已知数据是30个，所以位置的交换有30*29/2=435种。
整个交换的执行流程如下：
1、建立一个尝试字典集tryDic,键是数独的表达式,值是数独的结果的可能个数。
2、30个位置进行组合，生成435个包含两个位置的集合。
3、数独表达式交换前后分别记为before,after,解的个数分别记作b,a,将before,after及其结果数存入tryDic。
4、对435个集合进行遍历,若a!=0,且a小于b,则before=after;
5、很有可能第一轮排列组合之后,a并不等于1;没有找到唯一解的数独表达式,选取tryDic的结果个数最多的字符串S出来作为下一轮循环的因子。
6、循环执行1~5的过程，注意步骤5中的字符串S应该是过往循环中没有使用过的，否则会陷入死循环。

书上以

001000009000200046007080000000001000003000200000500000000030800960007000200000500

这个18个提示数的数独作为例子作为讲解，我也通过以上流程生成了一个18个提示数的标准数独。

借助书上的说法,除了聪明和运气，我们别无他法。

标准数独(元旦快乐)

最终生成的结果如下，难度不大。

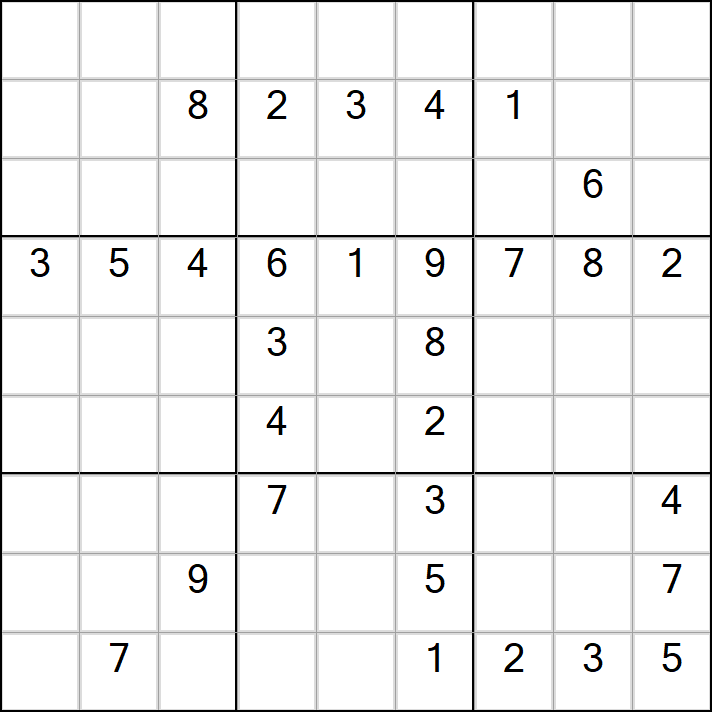
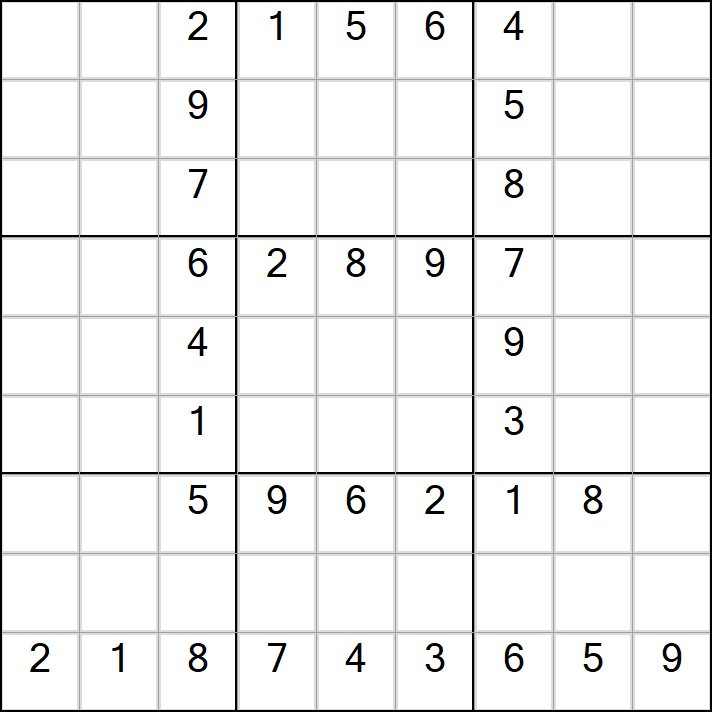
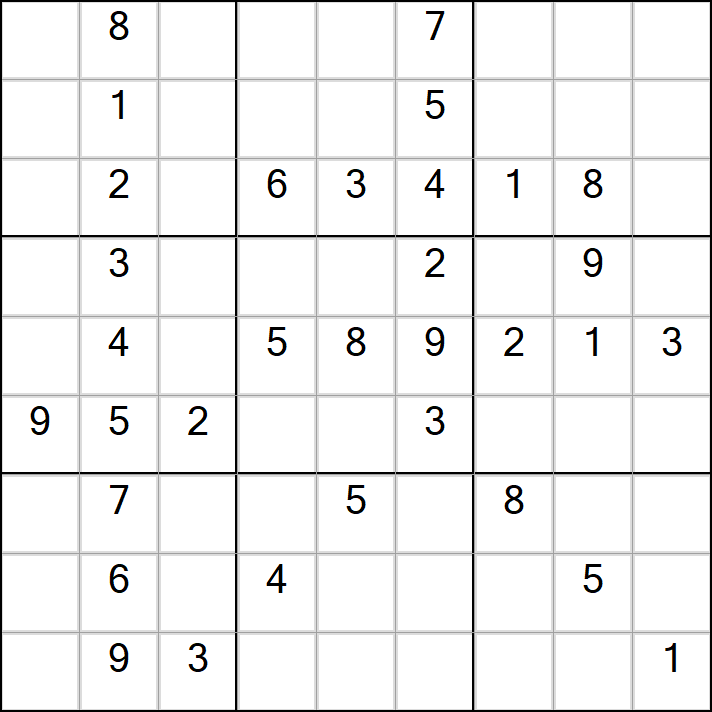
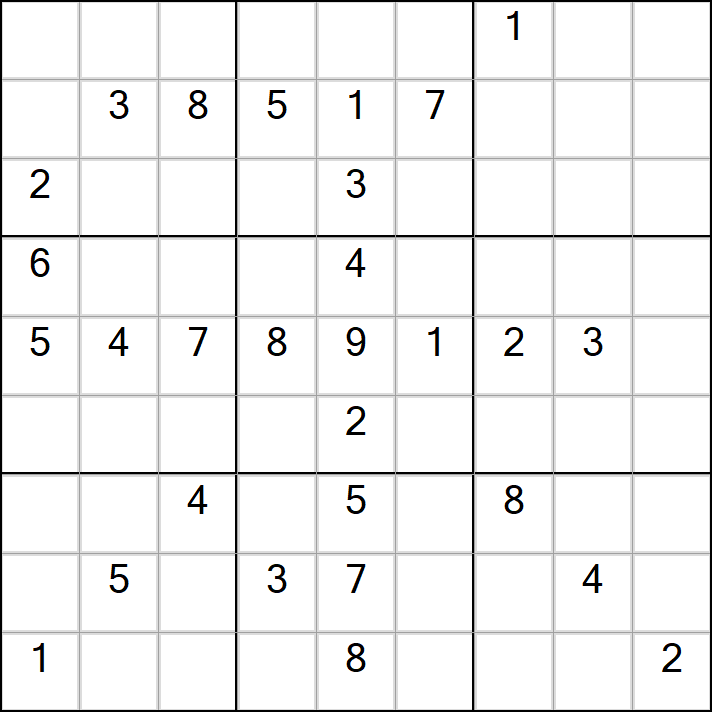
逆向思维

由以上位置找固定数独的位置可知，如果标准数独去掉某个提示数，不在构成唯一解，但是满足构成标准数独的基本条件,则可能通过两两交换的生成一个新的标准数独。

参考资料

• C#实现排列、组合
• C#源码